파이썬을 이용한 몬테카를로 시뮬레이션으로 ELS 밸류에이션(신영 ELS 190호)

ELS란?

ELS는 간단하게 설명해서 증권사와 내기하는 것이라 생각하면 간단하다.

정말 간단하게 예를들어 삼성전자가 2021년 내에 10만원을 터치하면 투자자에게 5%, 2022년내에 10만원을 터치하면 투자자에게 10%를 준다는 계약을 한다는것도 ELS라고 할 수 있다.

ELS란 무엇인가

ELS 밸류에이션

이번 포스팅은 카이스트 금융공학석사 수업중 시뮬레이션 방법론 수업내에 있는 몬테카를로 시뮬레이션을 이용한 ELS 가치평가를 제가 이해한대로 설명해보고자 한다.

FDM이나 Brownian Bridge를 사용하여 데이터를 만들어도 되지만 제일 간단하고 직관적인 몬테카를로 시뮬레이션을 이용하고자 한다.

그리고 FDM은 자산이 3개 이상일때 데이터 생성속도가 매우 느려져 비효율적이다.

활용 데이터는 내가 만든 수정주가 데이터를 이용한다.

수정주가 데이터

밸류에이션할 ELS는 신영증권에서 발행한 190호를 사용한다.

위의 사진을 보면 한국전력과 하나금융지주의 주가를 이용한 상품인것을 알 수 있다.

데이터 불러오기

import pandas as pd
import numpy as np
import datetime
data=pd.read_csv("KRX_adj_except_div.csv",encoding="CP949",index_col="Unnamed: 0")

data에 전종목 주가가 들어 있다. 데이터 링크는 위에 올려놓았다.

한국전력과 하나금융지주 데이터 분리

ELS_data=data[["015760","086790"]]
ELS_before_start=ELS_data.loc["20060518":].dropna()
ELS_after_start=ELS_data.loc["20080518":"20060518"]

ELS 존속기간동안의 데이터와 기준가격 결정일 전의 데이터를 저장한다. 저장하는 이유는 두 주식간의 상관관계와 일간변동성을 측정 해야하기 때문이다.

##ELS상장전 일별데이터를 이용한 sigma1, sigma2, correlation계산

##일별 등락폭을 이용 ->일별 등락폭의 분포가 미래에도 비슷 할것이라 예상
ELS_before_start["015760"]=ELS_before_start["015760"]/ELS_before_start["015760"].shift(-1)
ELS_before_start["086790"]=ELS_before_start["086790"]/ELS_before_start["086790"].shift(-1)

corr=ELS_before_start.corr().iloc[0,1]
sigma1=ELS_before_start["015760"].std()
sigma2=ELS_before_start["086790"].std()
print(sigma1,sigma2,corr)

sigma1은 한국전력의 일별변동폭의 표준편차, sigma2는 하나금융지주의 일별변동폭의 표준편차이고, corr은 두 종목의 일별변동폭의 상관계수이다.

과거 데이터를 이용할때는 시장이 급변하는 상황을 반영하지 못하기 때문에 valuation결과는 이를 고려하여야한다.

두 주식의 일별 변동폭을 히스토그램으로 비교

#한국전력의 일별 수익률 분포 
(ELS_before_start["015760"]-1).hist(bins=20)
#하나금융지주의 일별 수익률 분포 
(ELS_before_start["086790"]-1).hist(bins=20)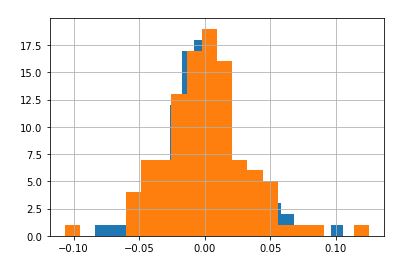

비교를 하는 이유는 종모양이 나오지 않을 경우 시뮬레이션 하는 의미가 없기 때문이다.

몬테 카를로 시뮬레션을 이용한 가상 데이터 생성

n_days=ELS_after_start.shape[0]      ### 만들 데이터 크기 정의
div1=0 ##배당률은 0으로 가정
div2=0
r=0.05/365 #무위험 이자율
T=1 #일간 변동성을 이용하여 데이터를 만드는 것이므로 T==1
simul_data1=np.ones(n_days)
simul_data2=np.ones(n_days)
x1=np.random.normal(size=n_days)     ### 정규분포 (0,1) 생성
x2=np.random.normal(size=n_days)

e1=x1
e2=corr*x1+x2*np.sqrt(1-pow(corr,2))  ###몬테카를로 변수

###가상 데이터 생성 
simul_data1=simul_data1/np.exp((div1-r-pow(sigma1,2)/2)*T+sigma1*e1*np.sqrt(T))
simul_data2=simul_data2/np.exp((div2-r-pow(sigma2,2)/2)*T+sigma2*e2*np.sqrt(T))

simul_data=pd.DataFrame(columns=ELS_after_start.columns,index=ELS_after_start.index)
simul_data["015760"]=simul_data1
simul_data["086790"]=simul_data2
simul_data.index = pd.to_datetime(simul_data.index, format = '%Y%m%d')
simul_data.plot()

위의 코드를 실행하면 몬테 카를로 시뮬레이션을 이용한 미래 2년간의 일별 예상 수익률데이터가 simul_data에 저장된다.

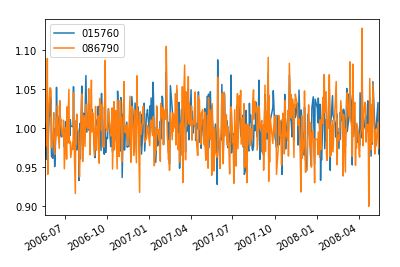
위의 사진은 한국전력과 하나금융지주의 일별 예상 수익률 데이터를 plot한것이다.

수익률 누적곱을 이용한 가상 주가 데이터 생성

simul_data["015760"][::-1].cumprod().plot()
simul_data["086790"][::-1].cumprod().plot()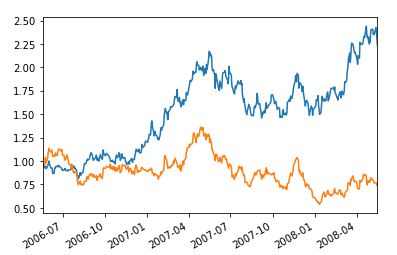

simul_data에서 생성된 일별 수익률 데이터를 누적곱을 해주면 2년간의 일별 예상 주가 데이터가 생성된다.

누적곱 데이터를 저장

simul_data["015760"]=simul_data["015760"][::-1].cumprod()[::-1]
simul_data["086790"]=simul_data["086790"][::-1].cumprod()[::-1]
simul_data=simul_data[::-1]

케이스 별로 수익을 추정

case=0

time1=simul_data.index[0]+datetime.timedelta(days=186)
time2=simul_data.index[0]+datetime.timedelta(days=365)
time3=simul_data.index[0]+datetime.timedelta(days=365+185)
time4=simul_data.index[0]+datetime.timedelta(days=365+364)
profit=0
if simul_data["015760"].loc[time1]>0.85 and simul_data["086790"].loc[time1]>0.85:
    case=1
    profit=pow(1.125,0.5)/pow(1+r*365,0.5)
elif simul_data["015760"].loc[time2]>0.8 and simul_data["086790"].loc[time2]>0.80:
    case=2
    profit=pow(1.125,1)/pow(1+r*365,1)
elif simul_data["015760"].loc[time3]>0.75 and simul_data["086790"].loc[time3]>0.75:
    case=3
    profit=pow(1.125,1.5)/pow(1+r*365,1.5)
elif simul_data["015760"].loc[time4]>0.70 and simul_data["086790"].loc[time4]>0.70:
    case=4
    profit=pow(1.125,2)/pow(1+r*365,2)
### 60퍼 이상 하락한적이 없는경우
if simul_data[simul_data<0.6].dropna().shape[0]==0 and (simul_data["015760"].loc[time4]<0.70 or simul_data["086790"].loc[time4]<0.70 ):
    case=5
    profit=1/pow(1+r*365,2)
### 60퍼 이상 하락한적이 있는경우
if simul_data[simul_data<0.6].dropna().shape[0]!=0 and (simul_data["015760"].loc[time4]<0.70 or simul_data["086790"].loc[time4]<0.70 ):
    case=6
    profit=min(simul_data["015760"].loc[time4],simul_data["086790"].loc[time4])/pow(1+r*365,2)
print(case,profit)

이 부분이 제일 중요하다. 맨위의 사진을 다시 보면 “매 6개월 마다 두 종목의 조기상환평가가격이 모두 기준가격의 85%(6개월), 80%(12개월),75%(18개월), 70%(24개월) 이상인 경우 연 [12.5]%의 수익으로 자동 조기상환 결정” 이라는 문구를 볼수 있다. 이를 각각 case1,2,3,4로 나누어 수익률을 현가로 환산하여 가격 데이터에 저장한다.

또한 “만기까지 한 종목도 장중가 포함하여 기준가격의 [60]%미만으로 하락한 적이 없고, 만기평가 가격이 한 종목이라도 기준가격의 [70]% 미만인 경우: 원금 지급” 이라는 문구는 case 5로 분류를 하였고, “만기까지 한 종목이라도 장중가 포함하여 기준가격의 [60]% 미만으로 하락한 적이 있고, 만기평가가격이 한 종목이라도 기준가격의 [70]% 미만인 경우: 원금 x (각 기초자산의 [만기평가가격]/[기준가격] 중 최소값)을 지급” 이라는 문구에서 case 6을 도출할수 있다. 이는 코드를 읽어보면 다 구현 해놓았다.

이는 시뮬레이션 데이터를 단 1개만 생성하여 case를 나눈경우로 이를 100개 1000개를 생성하여 case별로 수익을 계산해보면 미래 ELS가격의 현가를 알 수 있다.

N개의 데이터를 생성

##몬테 카를로 시뮬레션을 이용한 가상 데이터 생성

n_days=ELS_after_start.shape[0]      ### 만들 데이터 크기 정의
div1=0 ##배당률
div2=0
r=0.05/365 #무위험 이자율
T=1 #일간 변동성을 이용하여 데이터를 만드는 것이므로 T==1

#N개의 시뮬레이션 생성
N=100
simul_data1=np.ones((n_days,N))
simul_data2=np.ones((n_days,N))
x1=np.random.normal(size=(n_days,N))     ### 정규분포 (0,1) 생성
x2=np.random.normal(size=(n_days,N))

e1=x1
e2=corr*x1+x2*np.sqrt(1-pow(corr,2))  ###몬테카를로 변수
simul_data1=simul_data1/np.exp((div1-r-pow(sigma1,2)/2)*T+sigma1*e1*np.sqrt(T))
simul_data2=simul_data2/np.exp((div2-r-pow(sigma2,2)/2)*T+sigma2*e2*np.sqrt(T))

N개의 데이터를 생성하였다.

N개의 데이터를 case별로 나누어 현가 계산

case_list=[]
profit_list=[]
for i in range(N):
    simul_data=pd.DataFrame(columns=ELS_after_start.columns,index=ELS_after_start.index)
    simul_data["015760"]=simul_data1[:,i]
    simul_data["086790"]=simul_data2[:,i]
    simul_data.index = pd.to_datetime(simul_data.index, format = '%Y%m%d')
    simul_data["015760"]=simul_data["015760"][::-1].cumprod()[::-1]
    simul_data["086790"]=simul_data["086790"][::-1].cumprod()[::-1]
    simul_data=simul_data[::-1]

    case=0

    time1=simul_data.index[0]+datetime.timedelta(days=186)
    time2=simul_data.index[0]+datetime.timedelta(days=365)
    time3=simul_data.index[0]+datetime.timedelta(days=365+185)
    time4=simul_data.index[0]+datetime.timedelta(days=365+364)
    profit=0
    if simul_data["015760"].loc[time1]>0.85 and simul_data["086790"].loc[time1]>0.85:
        case=1
        profit=pow(1.125,0.5)/pow(1+r*365,0.5)
    elif simul_data["015760"].loc[time2]>0.8 and simul_data["086790"].loc[time2]>0.80:
        case=2
        profit=pow(1.125,1)/pow(1+r*365,1)
    elif simul_data["015760"].loc[time3]>0.75 and simul_data["086790"].loc[time3]>0.75:
        case=3
        profit=pow(1.125,1.5)/pow(1+r*365,1.5)
    elif simul_data["015760"].loc[time4]>0.70 and simul_data["086790"].loc[time4]>0.70:
        case=4
        profit=pow(1.125,2)/pow(1+r*365,2)
    ### 60퍼 이상 하락한적이 없는경우
    if simul_data[simul_data<0.6].dropna().shape[0]==0 and (simul_data["015760"].loc[time4]<0.70 or simul_data["086790"].loc[time4]<0.70 ):
        case=5
        profit=1/pow(1+r*365,2)
    ### 60퍼 이상 하락한적이 있는경우
    if simul_data[simul_data<0.6].dropna().shape[0]!=0 and (simul_data["015760"].loc[time4]<0.70 or simul_data["086790"].loc[time4]<0.70 ):
        case=6
        profit=min(simul_data["015760"].loc[time4],simul_data["086790"].loc[time4])/pow(1+r*365,2)
    case_list.append(case)
    profit_list.append(profit)

case_list라는 변수에 각각 시뮬레이션상 몇개의 데이터가 case별로 나누어져있는지 볼수 있고 profit_list에는 각각의 시뮬레이션의 미래 결과를 볼수 있다. 즉 profit_list의 평균이 현재 이 ELS가격이 되는 것이다. profit_list의 평균은 약 0.933으로 미래 가격을 1로 생각했을때 약 6.6% 할인된 가격으로 사야 합리적인 가격으로 산다는 것이다. 즉 만기수익률이 7.1% 이하라면 ELS는 살 가치가 없는 것이다.